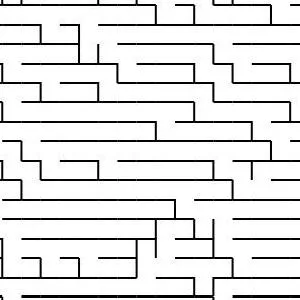
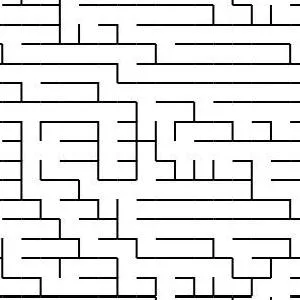
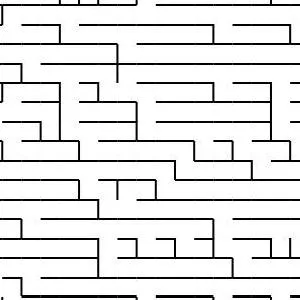
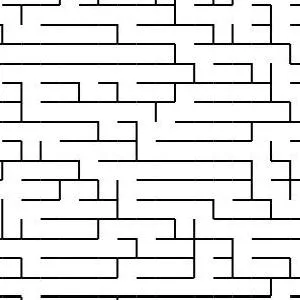
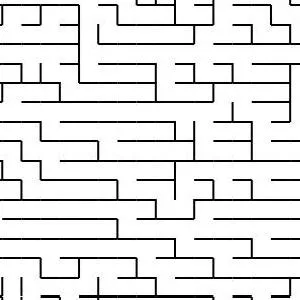
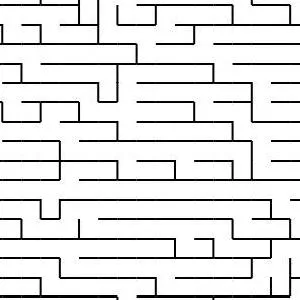
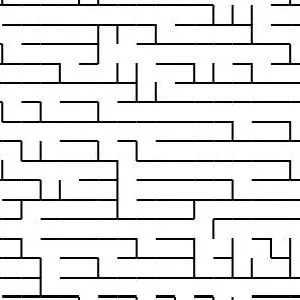
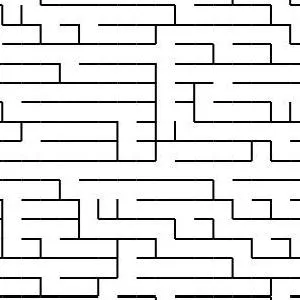
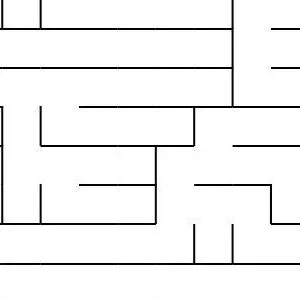
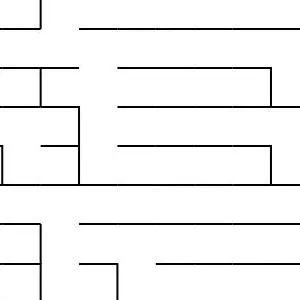
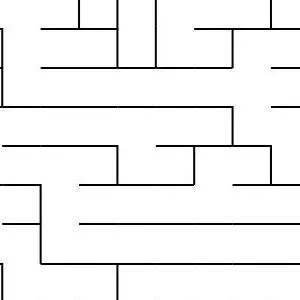
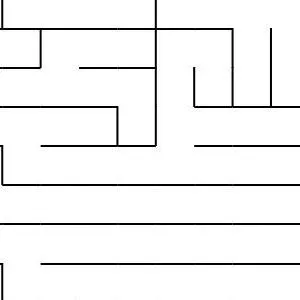
Generating Fractal Mazes: A Recursive Approach
Published: 2025-02-10

Fractal mazes are a fascinating concept, combining the complexity of fractal geometry with the challenge of a maze. They are constructed using a recursive process that allows the maze to exponentially grow while maintaining its structural integrity. Here’s how you can generate a fractal maze step by step:
1. Starting with the Base Maze
The first step is to define the initial maze. Typically, this base maze will be in two dimensions (though it could be generalized to higher dimensions) and will have a specific size. For instance, you can create a 10x10 grid maze. This maze will consist of walls and paths, with each cell in the maze either being part of the path or being a wall.
In our example, the 10x10 maze will have 100 cells, each of which is either empty (a path) or blocked (a wall). At this point, the maze is simple, but it serves as the starting point for the fractal generation.
2. Generating Sub-Mazes for Each Cell
Now, for each cell in the base maze, we create a new sub-maze that matches the dimensions of the original maze. So, for each of the 100 cells in the 10x10 grid, a new 10x10 maze is generated. These sub-mazes are identical in structure to the base maze.
The key principle in this step is that each sub-maze replaces the corresponding cell in the original maze. However, not all of the sub-maze’s walls and paths will be strictly the same. Here’s why:
If a wall exists in the base maze and there’s no wall in the corresponding direction of the sub-maze, we must make sure that the transition between the base maze and the sub-maze still respects the maze's structure. To do this, we will "open a path" in the sub-maze at the appropriate location, ensuring that the exit from one maze flows smoothly into the entrance of the next.
This recursive generation results in a maze that is exponentially larger, with the walls of the larger maze intact. However, instead of simply filling each cell with a uniform pattern, the process imbues the structure with a fractal-like complexity.
3. Recursive Expansion: Repeating the Process
Once the sub-mazes have replaced the cells in the original maze, you can repeat the process as many times as desired. Each time you do, the sub-mazes will themselves be replaced by new sub-mazes, further expanding the complexity of the maze. At each level of recursion, you are adding a new layer of mazes within mazes, with each cell of the maze now holding another maze inside it.
As you continue this recursive process, the maze grows at an exponential rate, but it still maintains the same basic structure. The walls from the original maze remain intact, and the paths inside each sub-maze are adjusted to allow for smooth transitions between the different layers.
This process creates a fractal-like structure, where smaller versions of the maze are nested inside larger ones, and each level of recursion adds more detail to the overall maze without disrupting the larger maze’s structure.
4. Resulting Structure
At the end of the recursion, you end up with a highly intricate and exponentially large fractal maze. The key feature of this maze is that it’s a self-similar structure, meaning each part of the maze resembles the whole, but with an increasing level of detail at each deeper level.
For example, a 10x10 maze with three levels of recursion could have 10,000 cells at the third level, each of which is a sub-maze that fits the pattern of the original maze. The complexity grows rapidly, but the design and structure remain cohesive, making it a visually captivating and challenging puzzle.
5. Final Thoughts
Fractal mazes are an elegant way of combining geometry and pathfinding. By repeating a simple recursive process, we can create mazes that increase exponentially in complexity while maintaining a coherent and harmonious structure. The beauty of fractal mazes lies in their infinite levels of detail, making them an ideal playground for both algorithmic exploration and design.
In practice, generating such mazes is not just about creating large mazes but about observing how recursive structures can emerge from simple rules. Whether you're designing a puzzle game, exploring fractal geometry, or studying the concept of self-similarity, fractal mazes offer a powerful example of how complexity can arise from simplicity.
Buy NSFW Adult Images
Blog

|
Generating Fractal Mazes: A Recursive Approach |